Right Triangular Pyramid Volume Calculator
| Result: |
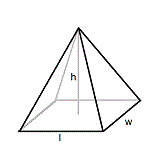
Volume of a Right rectangular pyramid = 1/6 * ( Area of rectangle * height )
Choose the shape you want to calculate the volume of:
Pyramid Volume Calculator
Discover the simplicity of calculating the volume of right triangular pyramids with our user-friendly online calculator. Perfect for students, architects, and professionals needing precise measurements for their projects.
What is a Right Triangular Pyramid?
A right triangular pyramid is a three-dimensional solid with a triangular base and triangular sides that meet at a point above the base. This point is called the apex. The right triangular pyramid is unique because it has a right angle in its base.
How Does the Pyramid Volume Calculator Work?
Our calculator simplifies the process of finding the volume of a right triangular pyramid. Enter the length and width of the pyramid's base and its height from the base to the apex to get the volume instantly.
Formula for Calculating Volume
The volume of a right triangular pyramid is given by:
\[ \text{Volume} = \frac{1}{6} \times (\text{Area of the base} \times \text{Height}) \]
The area of the base (a right triangle) is calculated as:
\[ \text{Area of base} = \frac{1}{2} \times \text{Base} \times \text{Height of base} \]
Uses and Applications
Right triangular pyramids are studied in geometry and are significant in various fields including architecture, construction, and education. They help in understanding geometric principles and are used in designing roofs, pyramids, and tetrahedral structures.
Frequently Asked Questions
How do you find the volume of a right triangular pyramid?
To calculate the volume of a right triangular pyramid, use the formula \( \text{Volume} = \frac{1}{6} \times (\text{base area} \times \text{height}) \). The base area for a right triangle is \( \frac{1}{2} \times \text{base length} \times \text{height of the base} \).
What is the formula for a right triangle pyramid?
The formula for a right triangle pyramid, which is a specific case of a triangular pyramid with a right-angled base, is \( \text{Volume} = \frac{1}{6} \times (\text{base area} \times \text{height}) \).
What is the formula for volume of a triangular pyramid calculator?
The volume formula for any triangular pyramid is \( \text{Volume} = \frac{1}{3} \times \text{base area} \times \text{height} \). The base area can be calculated based on the shape of the base triangle.
What is the formula for the volume of a right pyramid?
For a right pyramid (a pyramid with the apex directly above the center of the base), the volume formula is \( \text{Volume} = \frac{1}{3} \times \text{base area} \times \text{height} \).
What is the volume of a right triangular prism example?
The volume of a right triangular prism can be calculated using \( \text{Volume} = \text{base area} \times \text{height} \), where the base area is the area of the right triangle at the base of the prism.
What is the volume of the right triangular based prism?
To find the volume, multiply the area of the triangular base by the prism's height. For a right triangle, this is \( \text{Volume} = \frac{1}{2} \times \text{base} \times \text{height of triangle} \times \text{height of prism} \).
How do you find the volume of a right triangular pyramid?
The volume of a right triangular pyramid is calculated using the formula \( V = \frac{1}{3} B h \), where \( B \) is the area of the base triangle, and \( h \) is the height of the pyramid from the base to the apex.
What is the formula for a right triangle pyramid?
For a right triangular pyramid, the volume formula is the same as above, with the base area calculated specifically for a right triangle.
What is the formula for volume of a triangular pyramid calculator?
The formula used in calculators for a triangular pyramid's volume is \( V = \frac{1}{3} B h \), ensuring to input the correct base area and pyramid height.
What is the formula for the volume of a right pyramid?
The volume formula for any right pyramid, including square and triangular bases, is \( V = \frac{1}{3} B h \).
What is the volume of a right triangular prism example?
The volume of a right triangular prism is calculated as \( V = B h \), where \( B \) is the base area of the triangle, and \( h \) is the height (length) of the prism.
What is the volume of the right triangular based prism?
For a right triangular based prism, the volume formula is \( V = \frac{1}{2} b h l \), where \( b \) and \( h \) are the base and height of the triangle, and \( l \) is the length of the prism.
What are the rules of right pyramid?
Rules of a right pyramid include a polygonal base and triangular faces that meet at a common point (the apex), which is directly above the centroid of its base.
Is a triangular pyramid a right triangle?
A triangular pyramid, also known as a tetrahedron, may not necessarily consist of right triangles. It has four triangular faces, which can be of any shape.
How do you find the area of a triangular pyramid on a calculator?
To find the area of a triangular pyramid (surface area), you sum the areas of all four triangles. The formula depends on the dimensions of the pyramid.
What is a formula of area of triangle?
The area of a triangle can be found using \( A = \frac{1}{2} b h \), where \( b \) is the base length, and \( h \) is the height.